LeetCode 1335 solution

You want to schedule a list of jobs in d days. Jobs are dependent (i.e To work on the ith job, you have to finish all the jobs j where 0 <= j < i).

You have to finish at least one task every day. The difficulty of a job schedule is the sum of difficulties of each day of the d days. The difficulty of a day is the maximum difficulty of a job done on that day.

You are given an integer array jobDifficulty and an integer d. The difficulty of the ith job is jobDifficulty[i].

Return the minimum difficulty of a job schedule. If you cannot find a schedule for the jobs return -1.

Example 1:

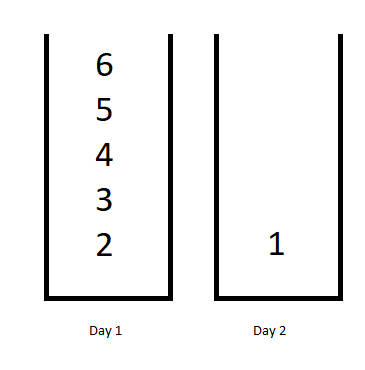
• Input: jobDifficulty = [6,5,4,3,2,1], d = 2
• Output: 7
• Explanation: First day you can finish the first 5 jobs, total difficulty = 6.
  Second day you can finish the last job, total difficulty = 1.
  The difficulty of the schedule = 6 + 1 = 7

python

def minDifficulty(jobDifficulty: List[int], d: int) -> int:
    n = len(jobDifficulty)
    if n < d: 
        return -1

    dp = [[float('inf')] * (n + 1) for _ in range(d + 1)]
    dp[0][n] = 0

    for day in range(1, d + 1):
        for i in range(n - day, -1, -1):
            max_diff = 0
            for j in range(i, n - day + 1):
                max_diff = max(max_diff, jobDifficulty[j])
                dp[day][i] = min(dp[day][i], max_diff + dp[day - 1][j + 1])

    return dp[d][0]

This code is designed to solve the "Minimum Difficulty of a Job Schedule" problem, which is a dynamic programming challenge.

Here's a breakdown of the code:

1. Function Definition:
   • def minDifficulty(jobDifficulty: List[int], d: int) -> int
     • This defines a function named minDifficulty that takes two parameters: jobDifficulty, which is a list of integers representing the difficulty of each job, and d, an integer representing the number of days to complete all jobs. The function returns an integer.
2. Initial Checks:
   • n = len(jobDifficulty)
     • This line calculates the length of the jobDifficulty list and stores it in n.
   • if n < d: return -1
     • This checks if the number of jobs is less than the number of days. If it is, the function returns -1, indicating that it's impossible to schedule the jobs within the given days.
3. Dynamic Programming Table Initialization:
   • dp = [[float('inf')] * (n + 1) for _ in range(d + 1)]
     • This line initializes a 2D list (matrix) called dp with dimensions (d + 1) x (n + 1). Each element is set to float('inf'), which represents a very high value (effectively infinity).
   • dp[0][n] = 0
     • This sets the base condition for the DP table. It means that there is no difficulty on the 0th day after completing all jobs.
4. Dynamic Programming Computation:
   • for day in range(1, d + 1):
     • This loop iterates through each day.
   • for i in range(n - day, -1, -1):
     • This nested loop iterates backwards through the jobs. The range (n - day, -1, -1) ensures that there are enough jobs left to fill the remaining days.
   • Inside the nested loops:
     • max_diff = 0
       • Initializes the maximum difficulty encountered on the current day to 0.
     • for j in range(i, n - day + 1):
       • Another nested loop to consider each job starting from i up to n - day.
     • max_diff = max(max_diff, jobDifficulty[j])
       • Updates max_diff to be the maximum of the current max_diff and the difficulty of the job at index j.
     • dp[day][i] = min(dp[day][i], max_diff + dp[day - 1][j + 1])
       • Updates the DP table. It calculates the minimum difficulty for completing i jobs in day days, considering the current job difficulty and the difficulty calculated for previous days.
5. Return Statement:
   • return dp[d][0]
     • Finally, the function returns the minimum difficulty for completing all jobs in d days, which is stored in dp[d][0].

In summary, the code uses dynamic programming to calculate the minimum difficulty required to schedule a given number of jobs over a specified number of days, where each job has its own difficulty level. The approach involves filling up a DP table with the minimum difficulties calculated based on the maximum difficulty of jobs done on each day.