LeetCode 2385 solution

problem

You are given the root of a binary tree with unique values, and an integer start. At minute 0, an infection starts from the node with value start.

Each minute, a node becomes infected if:

The node is currently uninfected.
The node is adjacent to an infected node.

Return the number of minutes needed for the entire tree to be infected.

Example 1:

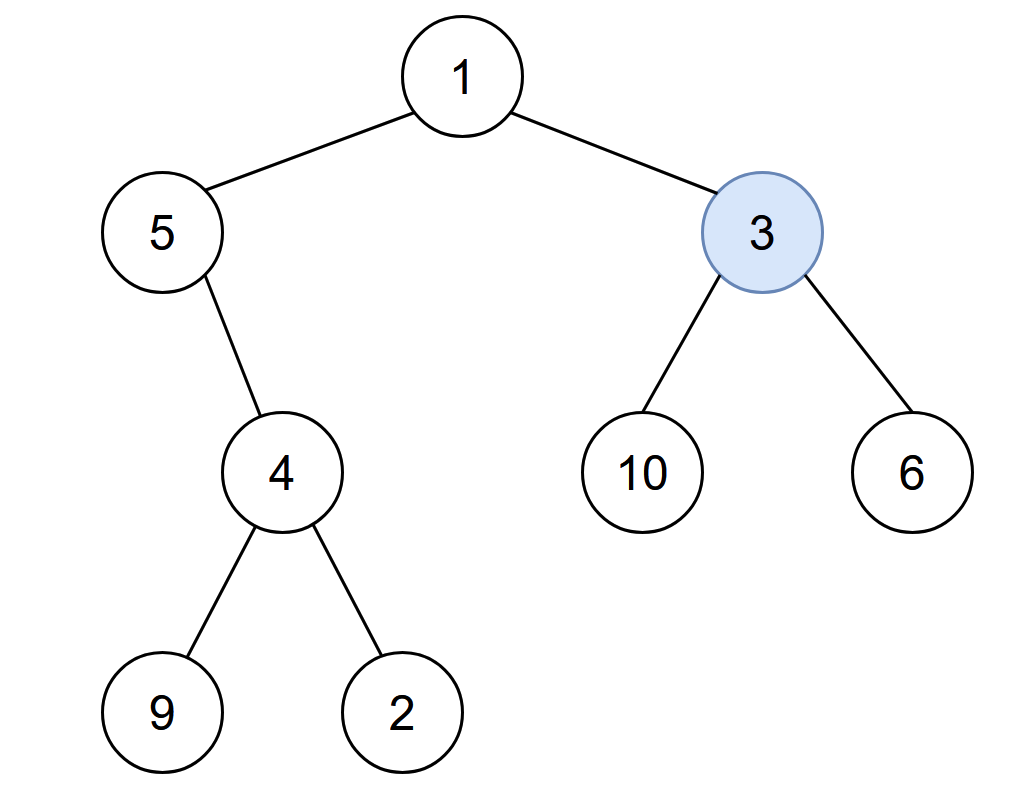
• Input: root = [1,5,3,null,4,10,6,9,2], start = 3
• Output: 4
• Explanation: The following nodes are infected during:
  - Minute 0: Node 3
  - Minute 1: Nodes 1, 10 and 6
  - Minute 2: Node 5
  - Minute 3: Node 4
  - Minute 4: Nodes 9 and 2
  It takes 4 minutes for the whole tree to be infected so we return 4.

python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

from collections import deque, defaultdict
class Solution:
    def amountOfTime(self, root: Optional[TreeNode], start: int) -> int:
        graph = defaultdict(list)
        def build_graph(node,parent):
            if node:
                if parent:
                    graph[node.val].append(parent.val)
                    graph[parent.val].append(node.val)
                build_graph(node.left,node)
                build_graph(node.right,node)
        build_graph(root,None)

        max_time = 0
        visited = set()
        queue = deque([(start,0)])
        while queue:
            node,time = queue.popleft()
            if node in visited:
                continue
            visited.add(node)
            max_time = max(max_time,time)
            for neighbor in graph[node]:
                if neighbor not in visited:
                    queue.append((neighbor,time+1))
        return max_time

1. 트리를 그래프로 변환: 먼저, 주어진 이진 트리를 그래프로 변환합니다. 각 노드의 양방향 연결을 저장하는 해시맵(또는 딕셔너리)을 사용하여 이를 구현합니다.
2. BFS 초기화: 시작 노드부터 BFS를 시작합니다. 이를 위해 큐를 사용하고, 시작 노드를 큐에 넣습니다.
3. BFS 수행: 큐에서 노드를 하나씩 꺼내면서 각 노드의 인접 노드들을 확인하고, 아직 감염되지 않은 노드를 큐에 추가합니다. 각 노드가 감염될 때까지 걸린 시간을 기록합니다.
4. 최장 감염 시간 계산: BFS를 수행하며 각 노드가 감염되기까지 걸린 시간 중 최댓값을 찾습니다. 이 최댓값이 전체 트리가 감염되는 데 필요한 시간입니다.

java

import java.util.*;

// Definition for a binary tree node.
class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int x) { val = x; }
}

public class Solution {
    public int amountOfTime(TreeNode root, int start) {
        // 트리를 그래프로 변환
        Map<Integer, List<Integer>> graph = new HashMap<>();
        buildGraph(root, null, graph);

        // BFS 수행
        Queue<int[]> queue = new LinkedList<>(); // [노드 값, 시간]
        Set<Integer> visited = new HashSet<>();
        queue.offer(new int[]{start, 0});
        int maxTime = 0;

        while (!queue.isEmpty()) {
            int[] current = queue.poll();
            int nodeVal = current[0], time = current[1];

            if (!visited.add(nodeVal)) {
                continue;
            }

            maxTime = Math.max(maxTime, time);

            for (int neighbor : graph.getOrDefault(nodeVal, Collections.emptyList())) {
                if (!visited.contains(neighbor)) {
                    queue.offer(new int[]{neighbor, time + 1});
                }
            }
        }

        return maxTime;
    }

    // 그래프 구축을 위한 도우미 메서드
    private void buildGraph(TreeNode node, TreeNode parent, Map<Integer, List<Integer>> graph) {
        if (node != null) {
            if (parent != null) {
                graph.computeIfAbsent(node.val, k -> new ArrayList<>()).add(parent.val);
                graph.computeIfAbsent(parent.val, k -> new ArrayList<>()).add(node.val);
            }
            buildGraph(node.left, node, graph);
            buildGraph(node.right, node, graph);
        }
    }
}

이 코드에서 buildGraph 메서드는 주어진 이진 트리를 양방향 그래프로 변환합니다. BFS는 Queue를 사용하여 각 노드의 감염 시간을 계산하고, 최종적으로 가장 긴 감염 시간을 maxTime 변수에 저장합니다.

이 문제를 해결하는 데 필요한 시간 복잡도는 O(n)입니다, 여기서 n은 트리의 노드 수입니다. 이는 각 노드를 한 번씩만 방문하기 때문입니다.