LeetCode 938 Solution

Problem

Given the root node of a binary search tree and two integers low and high, return the sum of values of all nodes with a value in the inclusive range [low, high].

Example 1:

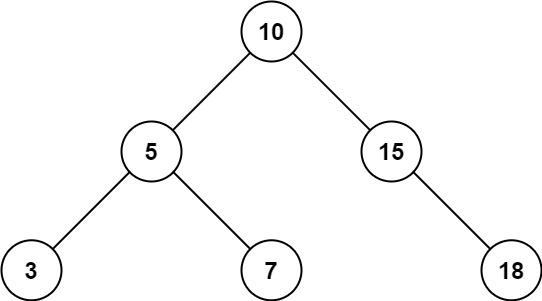
• Input: root = [10,5,15,3,7,null,18], low = 7, high = 15
• Output: 32
• Explanation: Nodes 7, 10, and 15 are in the range [7, 15]. 7 + 10 + 15 = 32.
  

Example 2:

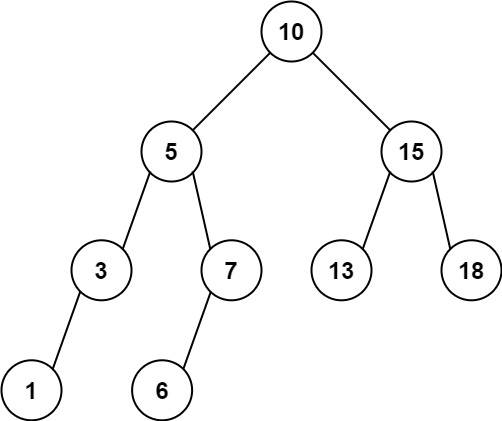
• Input: root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
• Output: 23
• Explanation: Nodes 6, 7, and 10 are in the range [6, 10]. 6 + 7 + 10 = 23.

Binary Search Tree

A Binary Search Tree (BST) is a fundamental data structure that's essential in computer science for efficient data storage and retrieval. Here are the key points that highlight its importance and functionality:

1. Definition and Structure:
   • A BST is a tree structure where each node can have up to two children, referred to as the left and right child.
   • The left child of a node always contains a value lesser than its parent node.
   • The right child always contains a value greater than its parent node.
   • This property must hold true for every subtree within the BST, not just the root.
2. Efficient Search and Sorting:
   • BSTs allow for efficient searching of data, as they leverage the property of binary search. In an average case, operations like search, insert, and delete have a time complexity of $O(log n)$.
   • Inorder traversal of a BST yields the elements in a sorted order, making it useful for tasks that require ordered data.
3. Imbalance Issues:
   • The efficiency of a BST can significantly deteriorate depending on the order of data insertion. For instance, inserting sorted data into a BST can lead to a skewed tree, resembling a linked list, where operations might take O(n) time.
   • Self-balancing binary search trees, such as AVL trees or Red-Black trees, are used to overcome this issue by maintaining a balanced height during insertions and deletions.
4. Deletion Operation:
   • Deleting a node in a BST can be more complex, especially if the node has children.
   • If the node is a leaf (no children), it is simply removed.
   • For a node with one child, the node is replaced with its child.
   • For a node with two children, the node is generally replaced with its in-order predecessor (the maximum value in the left subtree) or successor (the minimum value in the right subtree), and then that predecessor or successor is deleted.
5. Applications:
   • BSTs are utilized in various areas such as database management, file systems, and search engine optimization due to their efficiency in handling ordered data.

python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
        result = 0
        if root.val >= low and root.val <= high:
            result += root.val
        if root.left:
            result += self.rangeSumBST(root.left, low, high)
        if root.right:
            result += self.rangeSumBST(root.right, low, high)
        return result

1. Recursive search
   1. Use rangeSumBST recursively
2. Time complexity minimize
   1. $O(n)$ of time complexity